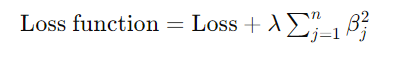Regularisation in Machine Learning: All you need to know

Summary: Regularisation methods like L1 (Lasso) and L2 (Ridge) curb overfitting by penalising model complexity. Elastic Net blends both approaches, while Dropout enhances neural networks by diversifying feature learning. These techniques ensure models perform well on new data, which is critical for robust Machine Learning applications.

Introduction

Preventing overfitting or underfitting during model training is crucial in Machine Learning. Hence, regularisation becomes pivotal. These techniques are vital in achieving this balance and creating an optimal model.

In this article, we will explore different types of regularisation in Machine Learning and how they help overcome overfitting and underfitting.

What is Regularisation in Machine Learning?

Regularisation in Machine Learning is a technique used to enhance model performance by preventing overfitting. Overfitting occurs when a model learns the noise in the training data instead of the actual patterns, leading to poor performance on unseen data. Regularisation adds a penalty to the model’s complexity, discouraging it from fitting the noise.

Regularisation techniques like L1 and L2 are vital in achieving a balanced and efficient Machine Learning model.

It helps create robust models that generalise new data well. Controlling the model’s complexity strikes a balance between underfitting and overfitting, leading to better predictive performance.

What is Overfitting in Machine Learning?

Overfitting in Machine Learning happens when a model learns not only the underlying pattern of the training data but also its noise and outliers. This results in a model that performs exceptionally well on training data but poorly on new, unseen data. 

Overfitting can occur due to an overly complex model with too many parameters relative to the number of observations. Techniques such as cross-validation, pruning, or regularisation can be employed to combat overfitting. Ensuring a balance between model complexity and generalisation ability is crucial for achieving robust performance on new datasets.

What is Underfitting in Machine Learning?

Underfitting in Machine Learning occurs when a model fails to capture the underlying patterns in the data. This happens because the model is too simple, unable to accurately represent the complexity of the data. 

As a result, it performs poorly on both the training data and unseen data, leading to high bias and low variance. Common causes of underfitting include using an insufficient number of features, an overly simplistic algorithm, or inadequate training time. 

To mitigate underfitting, one can increase model complexity, add more relevant features, or adjust hyperparameters to fit the data better.

Read Blog: Understanding Radial Basis Function In Machine Learning.

Types of Regularisation

Several regularisation methods exist, each with its unique approach and benefits. Here, we will explore the most commonly used regularisation techniques: L1 regularisation (Lasso), L2 regularisation (Ridge), Elastic Net, and Dropout.

L1 Regularisation (Lasso)

L1 regularisation, also known as Lasso (Least Absolute Shrinkage and Selection Operator), adds a penalty equal to the absolute value of the coefficients. This form of regularisation sets some of the coefficients to zero, effectively performing feature selection and leading to sparse models.

How L1 Regularisation Works

The L1 regularisation term is added to the loss function, which looks like this:

In this equation, the regularisation term   is added to the original loss function. Here, represents the model’s coefficients, and n is the number of coefficients. The parameter λ, known as the regularisation parameter, controls the strength of this penalty.

The role of λ is crucial:

• Higher λ values: When λ is large, the penalty increases, which results in more coefficients being shrunk towards zero. This effectively reduces the number of non-zero coefficients, promoting sparsity in the model. In other words, many coefficients will be precisely zero, simplifying the model by retaining only the most significant features.
• Lower λ values: Conversely, a smaller λ value results in a weaker penalty, allowing more coefficients to remain significant.

By carefully tuning λ, L1 regularisation can balance model complexity and performance, preventing overfitting and enhancing interpretability through feature selection.

Advantages of L1 Regularisation

L1 regularisation offers several advantages, making it a valuable tool in Machine Learning. By adding a penalty equal to the absolute value of the coefficients, L1 regularisation prevents overfitting, simplifies the model, and addresses multicollinearity. Here are the key benefits:

• Feature Selection: Lasso drives some coefficients to zero, effectively performing feature selection. This results in a simpler model that includes only the most relevant features, enhancing interpretability and reducing the risk of overfitting.
• Handling Multicollinearity: In high-dimensional datasets with correlated features, Lasso helps by selecting a subset of these features, mitigating the impact of multicollinearity and improving model stability.

Applications of L1 Regularisation

L1 regularisation is widely used in fields such as genetics, where the number of predictors (genes) can be much larger than the number of observations. Researchers often deal with thousands of genes in genetic studies, but only a few may be relevant to a particular disease or trait. 

L1 regularisation helps identify these key genes by shrinking the coefficients of less important ones to zero, effectively performing feature selection. This simplifies the model and makes it more interpretable, enabling researchers to focus on the most predictive genes and gain deeper insights into genetic associations and biological mechanisms.

L2 Regularisation (Ridge)

L2 regularisation, also known as Ridge regression, adds a penalty equal to the square of the magnitude of coefficients. Unlike L1 regularisation, Ridge does not set any coefficients to zero but shrinks them towards zero, ensuring all features contribute to the prediction.

How L2 Regularisation Works

The modified loss function with L2 regularisation looks like this:

In this equation, λ (lambda) is the regularisation parameter that controls the strength of the penalty. The term represents the sum of the squares of all the model’s coefficients. By adding this term to the loss function, L2 regularisation discourages the model from learning overly complex patterns that might fit the training data too closely.

A larger λ value increases the penalty, leading to greater coefficient shrinkage. This results in smaller coefficient values, which helps to reduce the model’s variance. In other words, by controlling the magnitude of the coefficients, L2 regularisation ensures that the model generalises better to new, unseen data.

L2 regularisation is an effective technique for improving the performance and robustness of Machine Learning models. It balances the trade-off between fitting the training data well and keeping the model’s complexity in check.

Advantages of L2 Regularisation

L2 regularisation is a powerful technique for improving the performance and robustness of Machine Learning models. It offers several key advantages that enhance the model’s ability to generalise to new data.

• Preventing Overfitting: L2 regularisation helps prevent overfitting by incorporating a penalty for large coefficients. This is particularly useful when the number of features is large, as it ensures that the model does not become too complex and fits the noise in the training data.
• Handling Multicollinearity: Ridge regression effectively addresses multicollinearity by shrinking correlated features together. This results in more stable and reliable estimates of the coefficients, which can improve the model’s predictive accuracy and interpretability.

Applications of L2 Regularisation

L2 regularisation is commonly use in scenarios with many predictors, such as text classification and image recognition. In text classification, it helps manage the vast number of features derived from text data, reducing overfitting and improving model generalisation. 

In image recognition, L2 regularisation ensures that the model learns from the essential features of the images without being overly influenced by noise or irrelevant details. By penalising large coefficients, L2 regularisation creates robust models that generalise to new, unseen data, enhancing their predictive performance in various complex tasks.

Elastic Net Regularisation

Elastic Net regularisation effectively blends the feature selection capabilities of L1 (Lasso) and the coefficient shrinkage of L2 (Ridge) regularisation. This dual-penalty approach is ideal for scenarios with numerous correlated predictors, allowing it to handle multicollinearity by grouping and selecting relevant sets of features.

How Elastic Net Regularisation Works

The loss function of Elastic Net is formulated by adding two components to the base loss: ​.

Here, λ1 and λ2​ are regularisation parameters that govern the strength of the L1 and L2 penalties, respectively. 

The L1 penalty encourages sparsity in the model by shrinking coefficients towards zero, facilitating feature selection. On the other hand, the L2 penalty ensures all features contribute by penalising large coefficients and handling multicollinearity.

By adjusting λ1 and λ2​, practitioners can fine-tune the balance between feature selection and model simplicity. Elastic Net regularisation is particularly effective in scenarios where datasets are high-dimensional and contain correlated features. 

This methodological flexibility and ability to address diverse data challenges make Elastic Net a widely used regularisation technique in Machine Learning and statistical modelling.

Advantages of Elastic Net Regularisation

Elastic Net regularisation blends the advantages of Lasso and Ridge techniques, offering a versatile approach to model regularisation in Machine Learning. Integrating L1 and L2 penalties effectively manages feature selection and simultaneously addresses multicollinearity challenges. This dual regularisation method provides several key benefits:

• Feature Selection: Enables the identification of relevant predictors by driving less influential coefficients to zero.
• Multicollinearity Handling: Mitigates the impact of correlated predictors, ensuring robust model performance.
• Flexibility in Tuning: Allows fine-grained control over the balance between L1 and L2 penalties through λ1 and λ2 parameters, facilitating optimal model tuning and enhancing predictive accuracy.

Applications of Elastic Net Regularisation

Elastic Net regularisation finds extensive application in fields like genomics and financial modelling due to its effectiveness in handling datasets with numerous predictors and potential multicollinearity issues. 

In genomics, where vast amounts of genetic data are analysed, Elastic Net aids in identifying relevant genetic markers while managing correlations between them. Similarly, in financial modelling, especially portfolio optimisation, Elastic Net helps select robust sets of financial instruments while considering their interdependencies. 

Its ability to balance between L1 (Lasso) and L2 (Ridge) penalties makes it particularly suitable for scenarios where feature selection and regularisation are critical for model stability and interpretability.

Dropout Regularisation

Dropout is a regularisation technique used primarily in neural networks. It involves randomly “dropping out” a fraction of the neurons during training, which prevents the network from becoming too reliant on particular neurons and encourages the network to learn more robust features.

How Dropout Regularisation Works

Dropout regularisation is a powerful technique for training neural networks to prevent overfitting. During each training iteration, a specified fraction 𝑝 of the neurons in the network is randomly set to zero. This stochastic process forces the network to learn redundant data representations, as it cannot rely heavily on any single neuron. 

The fraction 𝑝 is a hyperparameter that can be adjusted based on the complexity of the network and the dataset characteristics. This adjustment allows for flexibility in how aggressively or conservatively dropout is applied.

Notably, during testing or inference, dropout is not applied. Instead, the outputs of the neurons are scaled by 1 — 𝑝. This scaling compensates for the neurons that were dropped out during training, ensuring that the expected output of the network remains consistent across both training and testing phases.

Advantages of Dropout Regularisation

Dropout regularisation is a powerful technique in neural networks designed to combat overfitting and enhance generalisation. Dropouts introduce robustness into the network’s learning process by randomly disabling neurons during training. This approach offers several advantages:

• Preventing Overfitting: Dropout mitigates overfitting by preventing neurons from co-adapting too much, ensuring that no single neuron dominates the network’s learning.
• Improving Generalisation: By forcing the network to learn redundant representations, dropout encourages the discovery of more diverse features and patterns. This diversification enhances the model’s ability to generalise unseen data effectively, leading to more reliable predictions in real-world applications.

Applications of Dropout Regularisation

Dropout regularisation has found widespread application in various domains of deep learning, prominently in convolutional neural networks (CNNs) and recurrent neural networks (RNNs). Its effectiveness extends notably to critical tasks such as enhancing accuracy in image recognition by preventing overfitting and improving robustness in speech recognition systems. 

In natural language processing (NLP), dropout mitigates the risk of model reliance on specific word embeddings or sequences, thereby enhancing the generalisation capability of NLP models across diverse textual inputs. These applications underscore dropout’s versatility in fostering more reliable and adaptable deep learning architectures across different fields of artificial intelligence.

Choosing the Right Regularisation Technique

Choosing the right regularisation technique is critical in Machine Learning, as it directly impacts the model’s performance and ability to generalise to new data. Each regularisation method—L1, L2, Elastic Net, and Dropout—has specific strengths that align with data characteristics and modelling objectives.

When deciding on the appropriate regularisation technique:

• Use L1 Regularisation (Lasso): Opt for L1 regularisation when you suspect only a subset of features are crucial for prediction. By penalising the absolute values of coefficients, L1 regularisation encourages sparsity in the model, effectively performing feature selection. This is beneficial when dealing with high-dimensional data where feature relevance varies widely.
• Use L2 Regularisation (Ridge): Choose L2 regularisation when you want to include all features in the model but prevent them from over-influencing predictions, especially in multicollinearity. L2 regularisation penalises the squared magnitudes of coefficients, promoting smoother model outputs and reducing the impact of correlated features.
• Use Elastic Net: Employ Elastic Net when your dataset contains many correlated features. By combining L1 and L2 penalties, Elastic Net leverages the strengths of both methods, effectively handling multicollinearity while allowing for feature selection. This makes it a robust choice for datasets with complex relationships among predictors.
• Use Dropout: Implement Dropout specifically in neural networks to combat overfitting and enhance generalisation. By randomly dropping neurons during training, dropout forces the network to learn redundant representations and prevents it from relying too heavily on specific neurons, thereby improving model robustness.

By understanding these guidelines and assessing the specific characteristics of your data—such as feature importance, multicollinearity, and neural network architecture—you can strategically select the regularisation technique that best suits your modelling goals and improves your model’s performance on unseen data.

Further Read:
Discover Best AI and Machine Learning Courses For Your Career.

Machine Learning Interview Questions: Ace Your Next Interview.

Frequently Asked Questions

What is regularisation in Machine Learning?

Regularisation in Machine Learning involves adding a penalty to the model’s loss function to prevent overfitting. It adjusts the complexity of the model by penalising large coefficients, thereby promoting simpler models that generalise better to unseen data, improving overall predictive performance.

Which regularisation technique is best for feature selection?

L1 regularisation, known as Lasso, is highly effective for feature selection. It adds a penalty equal to the absolute value of coefficients, encouraging some coefficients to be precisely zero. This feature selection capability simplifies models by focusing on the most relevant features, enhancing interpretability and reducing overfitting.

How does dropout regularisation improve neural networks?

Dropout regularisation improves neural networks by randomly deactivating neurons during training. This technique prevents neurons from co-adapting too much to specific features, promoting the learning of diverse features. By forcing the network to be more robust, dropout reduces overfitting. It enhances the model’s ability to generalise to new data.

Conclusion

Regularisation techniques like L1, L2, Elastic Net, and Dropout are crucial in improving Machine Learning model performance. By balancing model complexity and preventing overfitting or underfitting, these methods ensure robust predictions of new data. 

L1 and L2 facilitate feature selection and control coefficient magnitudes, while Elastic Net blends their benefits for handling multicollinearity. Dropout, primarily for neural networks, enhances generalisation by diversifying feature learning. Understanding these techniques empowers Data Scientists to select the most suitable method based on data characteristics, fostering reliable and scalable Machine Learning models.