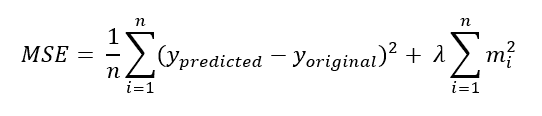Machine Learning is the area where computers are given the ability to learn without being explicitly programmed. Accordingly, it is one of the most exciting technologies that allows computers to think and work like humans, especially having the ability to learn. One of the most effective strategies of Machine Learning is Regularization that avoids overfitting. Effectively, Overfitting occurs when a model fits for data training too easily and is also complicated therefore fails to function adequately. Regularization is then used as a penalty into the model’s loss function. Moreover, has two different types of Regularizations, L1 and L2 Regularization in Machine Learning which will be discussed in the blog post.
What is Regularization in Machine Learning?
Regularization is the approach in Machine Learning that prevents overfitting by ensuring that a penalty term is included within the model’s function. There are two main objectives of Regularization include-
- To reduce the complexity of a model.
- To improve the ability of the model to generalise new inputs.
Numerous Regularization methods are used for adding different penalty terms which include L1 and L2 Regularization. While L2 Regularization is a punishment term based on the squares of the given parameters, L1 is a penalty term for absolute values of the model’s parameters. Certainly, with the help of Regularization, the chances of overfitting reduces and keeps the model’s parameters under control. Therefore, it helps enhance the model’s performance on untested data.
What is L1 Regularization?
L1 Regularization: Lasso Regularization is the strategy in Machine Learning that inhibits overfitting by introducing a penalty term in the model’s loss function. Consequently, the penalty term is based on the absolute values of the model’s parameters. L1 Regularization tends to reduce the parameters of some models to zero for lowering the number of non-zero parameters in the model.
L1 Regularization is useful when you need to work with high-dimensional data as it enables you to choose a subset of the most important attributes. Furthermore, it helps in reducing the risk of overfitting and makes the model easier to understand. The size of the penalty term is controlled by hyperparameter lambda which regulates the strength of L1 Regularization. Thus, improvement of the Regularization occurs when lambda rises and the parameters are reduced to zero.
The L1 Regularization formula is given below:
What is L2 Regularization?
L2 Regularization is known as Ridge Regularization, the approach in Machine Learning. It avoids overfitting by executing penalty terms in the model’s loss functions on the squares of the parameters of the model. The primary goal of L2 Regularization is to ensure that the parameter of the model has short sizes and prevents oversizing.
For achieving L2 Regularization. The term which is proportionate to the squares of the model’s parameters is added to the loss function. It works in limiting the size of the parameter and prevents them from growing out of control. The hyperparameter lambda which controls the Regularization’s intensity also ensure to control the size of the penalty term. The parameters hence will be smaller and the Regularization is stronger with the greater lambda.
The L2 Regularization formula is given below:
Differences Between L1 and L2 Regularization
While the two techniques are part of the Machine Learning approach, there are very
| L1 Regularization | L2 Regularization |
| The absolute values of the parameters of a model are what the penalty terms are based on. | The squares of the model parameters is what the penalty terms are based on. |
| Some of the parameters are reduced to zero hence producing sparse solutions. | The model uses all the parameters thus, producing non-sparse solutions. |
| Sensitive to outliers | Robust to outliers |
| It selects a subset of the most crucial features | All the features in this technique is useful for the model |
| Non-convex optimisation | Convex optimisation |
| The term of penalty is quite less sensitive to correlated features | The penalty term is highly sensitive to correlated features |
| It is useful while dealing with dimensional data | Useful while dealing with high dimensional data and when the goal is to have less complex model. |
| Also known as Lasso Regularization | Also known as Ridge Regularization |
Conclusion
L1 and L2 Regularization are the two different approaches in Machine Learning that prevent overfitting in the ML models. The above post makes it clear that the two different types of methods help in reducing complexities in the model and make improvements for better inputs. Certainly, L2 and L1 Regularization in Machine Learning enables it to work with high-dimensional data and keeps the model from getting into high complications. The differences prove that L1 Regularization is sensitive to outliers than L2 Regularization which are quite robust.