Time series data is the information or the data that is collected over a set period of time. It involves working on the most commonly used data by various organizations and industries. By analyzing the time series data, one can be able to get various insights, like trends, patterns, etc., from which we can be able to predict the future events. Thus helping in catalysing the growth of the company.
There are a few steps that should be taken care of while analyzing the time series data. You must be sure that stationarity and autocorrelation are checked and analyzed. Stationarity is a way to measure if the data has structural patterns like seasonal trends. Autocorrelation arises when future values in a time series analysis linearly depend on the previous or historical values. You need to check for both of these i.e., stationarity and autocorrelation in time series data as they are the assumptions that are made by many widely used methods in time series analysis. The time series data that is collected would be in years, months, days, etc. There are four types of components that are observed in time series analysis.
COMPONENTS OF TIME SERIES ANALYSIS
The major components of time series analysis are,
- Trend
- Seasonality
- Cyclical
- Irregularity
Let us explore the above components in detail!
Trend
The trend demonstrates the data’s overall tendency to increase or decrease over an extended period of time. One major point to consider is that the trend might increase, decrease, or even be constant in a given period of time, i.e., the overall trend must be upward, downward, or remain constant. An increase in the population, the number of education institutions or industries, an increase in the population, or a decrease or increase in demand for a product,a declining death rate, and population growth are some of the examples showing trends.
Linear Trend: If the pattern of the data is a straight line, either upward or downward or stable, then it is considered a linear trend.
Non-Linear Trend: If the pattern of the data has curves either upward or downward, then it is considered a non-linear trend.
Seasonal Variations
Seasonality is used to find the patterns or variations that occur at regular intervals of time, mostly on a yearly basis. Seasonal variations are the results of both natural and artificial events. They usually show the same pattern of upward or downward growth in the 12-month period of the time series. These variations are often recorded on an hourly, daily, weekly, quarterly, and monthly basis. Seasonality can be seen in the increase of room heater sales during the winter, fluctuations in fashion based on festivals and crop dependence on the season.
Cyclic Variations
Cyclical changes in a time series are those that persist for a longer period of time, usually more than a year. The oscillation time for this movement is greater than a year. A cycle consists of one full period. This oscillation is commonly referred to as the “business cycle.”
Prosperity, recession, depression, and recovery are the four phases that are present in the cyclical variation.Strikes, wars, floods, etc., are the examples of cyclical variations
Irregular Variations
Irregular or random variations are the patterns that are observed due to unpredictable or uncontrolled events that happen. As the name suggests, these variations do not follow any kind of regular time period. A rapid decrease in population due to a natural disaster is an example of an irregular variation.
STATIONARITY & NON-STATIONARITY OF TIME SERIES DATA
Stationarity
A time series is considered stationary when it is stable, which means
- The mean in the data during the analysis is constant over time (there is no trend).
- With respect to time, variation is constant.
- The autocorrelation remains constant over time
Non-Stationarity
The reverse of stationary data is non-stationary data. The mean, variance, and covariance of nonstationary data change over time. Trends, cycles, irregular patterns, or a combination of the three can be considered as non-stationary behaviours.
METHODS TO CHECK STATIONARITY
During the time series analysis model preparation process, we must check if the given dataset is stationary or not. In order to check the stationarity, below are a few methods or tests that can be performed.
Statistical Test: To determine if the dataset is stationary or not, there are two statistical tests that can be used. They are,
- Augmented Dickey-Fuller (ADF) Test
- Kwiatkowski-Phillips-Schmidt-Shin (KPSS) Test
Augmented Dickey-Fuller (ADF) Test or Unit Root Test: The ADF test is the most popular statistical test with the following assumptions.
- Null Hypothesis (H0): Data is non-stationary
- Alternate Hypothesis (HA): Data is stationary
- If p-value >0.05 then, fail to reject (H0)
- If p-value <= 0.05 , then accept (H1)
Kwiatkowski–Phillips–Schmidt–Shin (KPSS): This test is used for testing a NULL Hypothesis (HO), that will perceive the time-series as stationary around a deterministic trend against the alternative of a unit root. We must ensure that the dataset is steady because time series analysis needs stationary data for its additional analysis.
A series can be made stationary by various methods like:
- Difference Transform: Subtracting the previous value with the current value is called differencing. It is done to remove the dependency of values on time. The ADF test can be used to determine whether the differenced series is stationary.
- Differencing: If the result of the ADF test on the differenced series shows that the series is still non-stationary, then one can subtract the differenced series again.
- Removing trend and seasonality by using HP-filter, or band-pass filters and X12 ARIMA analysis.
ANALYZING TIME SERIES DATA
There are a few steps that need to be performed while analyzing the time series data. Let us quickly have a look at these steps.
- Collecting the dataset and performing data preprocessing
- Exploring the data using various visualization tools with respect to time vs key feature
- Checking for stationarity in the data
- Understanding the nature by creating charts
- Model building – AR, MA, ARMA and ARIMA
- Extracting insights from prediction
So, let’s implement some of the above steps using python.
TIME SERIES ANALYSIS IN PYTHON
Now let us see how to perform time series analysis in python. Here, we are using the dummy dataset which contains the number of travellers who travelled during a particular month and year.
Let us import the required libraries first.
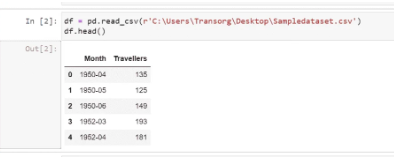
Now, let us read our dataset using the pandas library. Our dataset is in the form of a CSV (comma-separated values) file.
Now, I’m checking the datatype of the features present in the dataset.
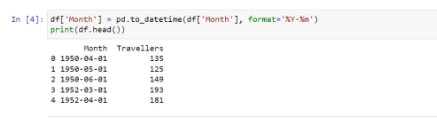
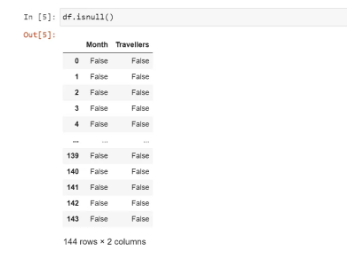
We found that the feature ‘Month’ is of the object type. So, we need to change it to datetime. Before that, let us check the missing values in the dataset.
Checking if there are any null values in the dataset
We found that there are no null values in the dataset. So, we changed the datatype of ‘Month’ to datetime.
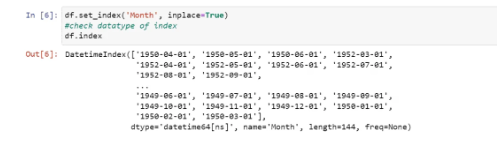
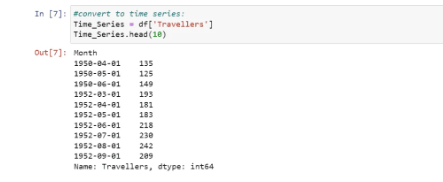
After performing the data preprocessing and changing the data types, we now need to convert our dataset to the time series data.
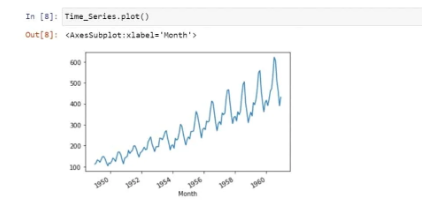
Next, we are going to visualize our time series data.
We have seen that there is a positive trend along with some seasonality in it. We are now checking for stationarity as it is an important step in the time series analysis.
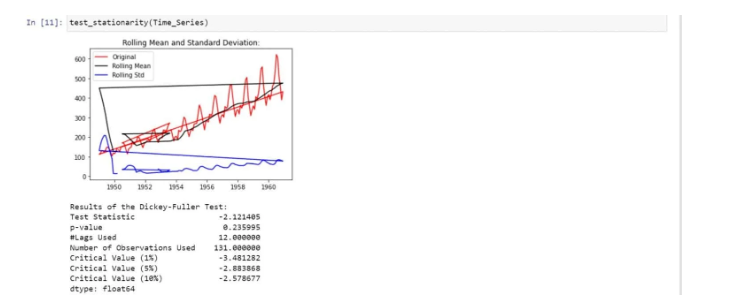
We have used a dickey-fuller test to check the stationarity. The Dickey-Fuller test is a type of statistical test used to check stationarity in the data.
We found that there is no stationarity in the data due to the following reasons:
- The mean is increasing even though the standard deviation is small.
- Test Statistics is greater than the critical value.
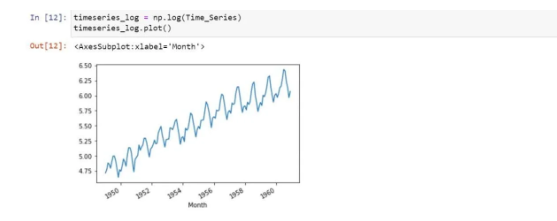
So, in order to make it stationarity, we are using logarithmic transformation.
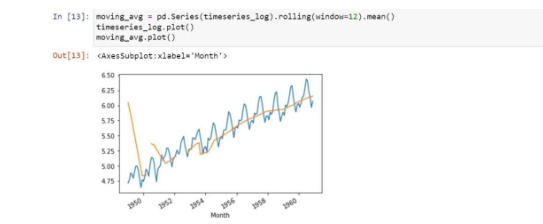
We found a positive or forward trend. In order to remove them, we are using the smoothing method. So, let’s use the moving averages method which is a type of smoothing method.
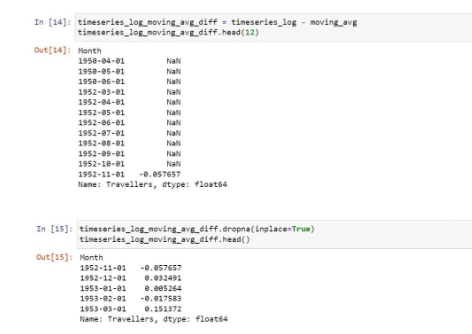
So, now we need to subtract the rolling mean from the original data.
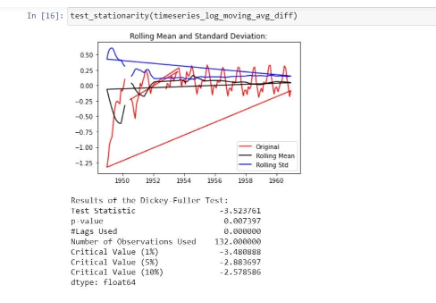
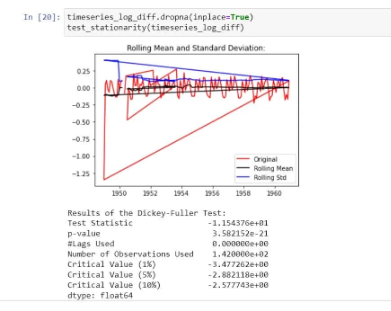
Now, let’s parse it to check for stationarity.
In the graph, we observe that there is no specific trend and even the test statistics is smaller than the critical value of 5%. That means, we can say it is stationary.
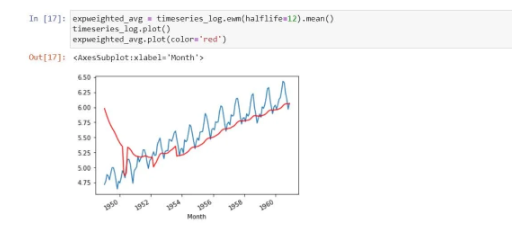
In the above process, we took an average of 12 months. But, sometimes, we need to work with a more complex range. The parameter (halflife) is assumed to be 12. Let’s check stationarity now,
We found that the above is stationary because the mean and standard deviation have fewer variations. At the same time, the test statistic is smaller than the 1% critical values.
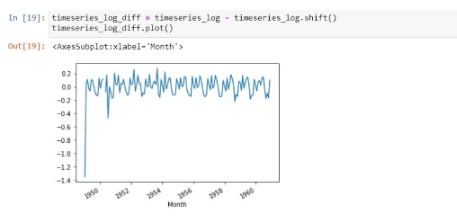
Let’s do the differencing now.
The above looks fine!
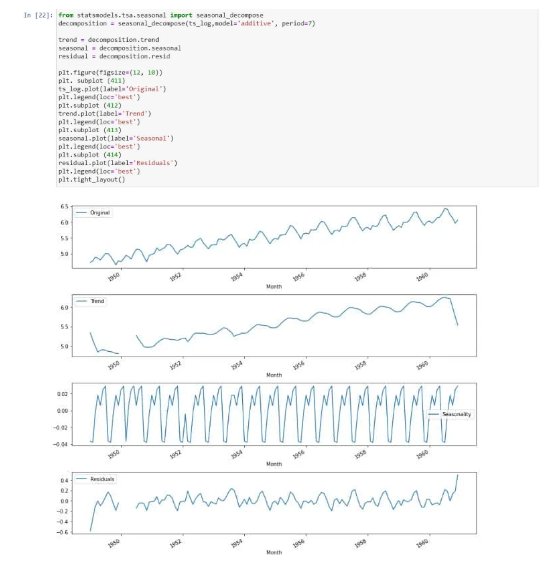
So, now just decompose the data into the components of time series. Here we model both the trend and the seasonality, and then the remaining part of the time series is returned.
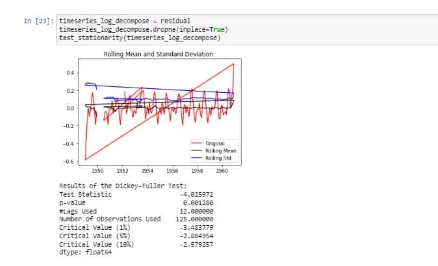
We can now use the residual values after removing the trend and seasonality from the time series. Check stationarity now.
The above is stationarity because the test statistic is less than the critical values and the mean, and standard deviation have very few variations with respect to time.
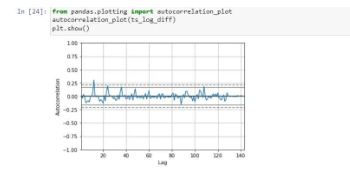
At last, we are visualizing the autocorrelation.
We have seen how to change the original data to time series and checking for stationarity, etc., using python. So, python makes it easy to analyze the time series data without any hassles.
CONCLUSION
Almost every data scientist will has to perform time series data analysis at some point in their career. Data scientists can find trends, foresee occurrences, and subsequently guide decision-making by having a solid understanding of the tools and methodologies for analysis. Promotional planning can be made more profitable for businesses by using stationarity, autocorrelation, and trend decomposition to understand seasonality patterns.
In conclusion, using time series forecasting to foresee future events in your time series data can have a big influence on decision-making. Any data scientist or data science team looking to use time series data to add value to their business will find these kinds of analyses to be extremely helpful.
I hope you enjoyed the blog. Now, it’s your time to implement the time series analysis!
Author
-
Written by:
Aishwarya Kurre
