How Cost Functions Shape Machine Learning Models: A Deep Dive

Summary: Cost functions measure prediction errors in Machine Learning, guiding models to improve accuracy. Common types include MSE for regression and cross-entropy for classification. Choosing the right function impacts optimization, robustness, and performance, ensuring models align with data patterns and task requirements.

Introduction

Imagine teaching a child to ride a bicycle. The first few attempts are wobbly, resulting in falls and scraped knees. Each mistake helps the child adjust their balance and technique, gradually reducing errors until they ride smoothly. In Machine Learning, the cost function plays a similar role—it quantifies the “mistakes” a model makes and guides it to improve, ensuring more accurate predictions with each iteration.

 Key Takeaways

• Cost functions quantify prediction errors to guide model training and parameter updates.
• MSE is ideal for regression, penalizing large errors but sensitive to outliers.
• Cross-entropy optimizes classification by aligning predicted probabilities with true labels.
• Choice impacts model performance, balancing accuracy, speed, and outlier handling.
• Gradient descent relies on cost functions to iteratively minimize errors and refine models

What is the Cost Function?

A cost function in Machine Learning is a mathematical tool that measures the error or difference between a model’s predicted outputs and the actual target values. It serves as an objective metric, quantifying how well or poorly a model is performing.

By minimizing the cost function, Machine Learning algorithms adjust their parameters—such as weights and biases—during training to improve accuracy. The cost function acts as a guide, directing the model to learn patterns from the data and achieve better predictive performance over time. It is fundamental to optimization and model evaluation, making it a core concept in Machine Learning.

Types of Cost Functions

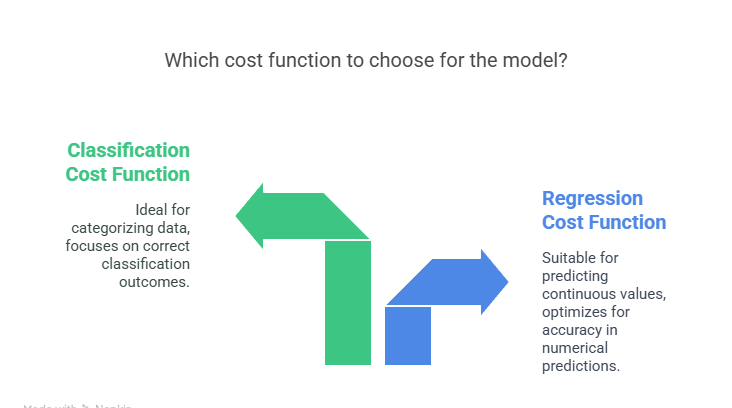
Cost functions vary based on the type of Machine Learning problem—regression or classification. The choice of cost function directly impacts how the model learns and optimizes its predictions.

Cost Functions for Regression

Regression problems involve predicting continuous values. Common cost functions include:

• Mean Squared Error (MSE): Calculates the average squared difference between predicted and actual values, heavily penalizing larger errors.
• Mean Absolute Error (MAE): Computes the average absolute difference, providing robustness against outliers.
• Huber Loss: Combines the advantages of MSE and MAE, being less sensitive to outliers than MSE but differentiable everywhere, unlike MAE.

These cost functions help the model learn by quantifying how far its predictions deviate from actual values, guiding parameter updates accordingly.

Cost Functions for Classification

Classification tasks assign data points to discrete categories. Common cost functions include:

• Binary Cross-Entropy (Log Loss): Used for binary classification, measuring the difference between predicted probabilities and actual binary outcomes.
• Categorical Cross-Entropy: Extends binary cross-entropy for multi-class classification, comparing predicted probabilities across multiple classes.
• Hinge Loss: Used in support vector machines (SVM), penalizing predictions that are not only incorrect but also not confident enough.

These functions ensure the model’s probability outputs align closely with true class labels, optimizing classification accuracy.

How Cost Functions Impact Model Training

Cost functions are central to the training process in Machine Learning. During training, the model makes predictions on the training data, and the cost function quantifies the error between predictions and actual outcomes. 

Optimization algorithms then use this error metric to adjust model parameters, aiming to minimize the cost. This iterative process continues until the cost function reaches its minimum or meets a stopping criterion, resulting in a model that generalizes well to unseen data. The choice and behaviour of the cost function directly influence how quickly and effectively the model learns.

Optimization Techniques to Minimize Cost

Minimizing the cost function is the primary objective during model training. Two major categories of optimization techniques are widely used:

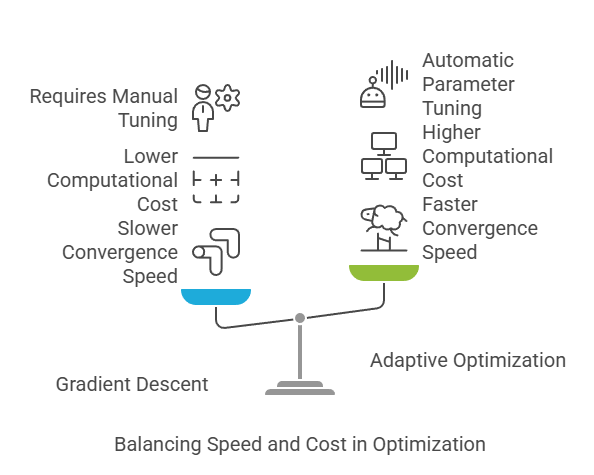
Gradient Descent

Gradient descent is the most common optimization algorithm in Machine Learning. It works by computing the gradient (partial derivatives) of the cost function with respect to the model parameters. 

The parameters are then updated in the opposite direction of the gradient, iteratively moving towards the minimum cost. Variants include batch, stochastic, and mini-batch gradient descent, each with different trade-offs in speed and stability.

Adaptive Optimization Methods

Adaptive methods, such as Adam, RMSprop, and Adagrad, build on gradient descent by adjusting the learning rate for each parameter based on historical gradients. These methods often lead to faster convergence and better performance, especially in Deep Learning and large-scale models. They help navigate complex cost landscapes and avoid issues like vanishing or exploding gradients.

Choosing the Right Cost Function

Selecting the appropriate cost function is a critical step in building effective Machine Learning models, as it directly influences how the model learns, optimizes, and performs on your specific task. There is no universal cost function suitable for all problems; the choice depends on several key factors:

Nature of the Problem

• Regression
  For predicting continuous values, cost functions like Mean Squared Error (MSE) or Mean Absolute Error (MAE) are commonly used. MSE penalizes larger errors more heavily, making it sensitive to outliers, while MAE is more robust in the presence of outliers.
• Classification
  For predicting discrete class labels, cross-entropy loss (binary or categorical) is widely used, especially in logistic regression and neural networks. Hinge loss is preferred for margin-based classifiers like Support Vector Machines (SVMs).

Data Characteristics

• Outliers
  If your dataset contains significant outliers, MAE or Huber loss may be preferable as they are less sensitive to extreme values compared to MSE.
• Imbalanced Data

When classes are imbalanced, consider cost functions that can be adjusted to penalize false positives and false negatives differently, or use weighted versions to ensure balanced performance across classes.

Model Architecture

• Neural Networks

The activation function and output layer often dictate the suitable cost function. For example, use binary cross-entropy with sigmoid activation for binary classification, and categorical cross-entropy with softmax activation for multi-class classification.

• Support Vector Machines

Hinge loss is specifically designed for SVMs, focusing on maximizing the margin between classes.

Computational Efficiency

Some cost functions are computationally simpler and faster to optimize. For very large datasets or real-time systems, choosing a cost function that balances accuracy and computational efficiency is important.

Regularization and Overfitting

Cost functions can be augmented with regularization terms (like L1 or L2 penalties) to discourage overly complex models and reduce overfitting, especially when dealing with high-dimensional data.

Conclusion

The cost function in Machine Learning is the critical feedback mechanism that tells a model how well it is performing and how it can improve. 

By quantifying errors and guiding the optimization process, cost functions ensure that models learn from their mistakes—just like a child mastering the art of riding a bike. 

Choosing the right cost function for your problem type is essential for building accurate, robust, and reliable Machine Learning models.

Frequently Asked Questions

What is the Difference Between a Cost Function and a Loss Function?

A loss function measures the error for a single data point, while a cost function typically represents the average error across the entire dataset. In practice, the terms are often used interchangeably in Machine Learning. 

How do I Choose The Right Cost Function for my Model?

Select a cost function based on your task: use MSE or MAE for regression, binary cross-entropy for binary classification, and categorical cross-entropy for multi-class classification. The choice impacts model performance and optimization.

Why is Minimizing the Cost Function Important in Machine Learning?

Minimizing the cost function ensures the model’s predictions closely match actual outcomes. This process improves accuracy, generalization, and reliability, making the model more effective for real-world applications and unseen data.